Department Personnel
Associate Professor Antonios Armaou | Research
Adaptive Model Reduction for control of PDEs
Significant research effort in recent years has been focused on the area of process control of distributed processes. This activity has been motivated by the wealth of industrially important processes (e.g. plasma-enhanced chemical vapor deposition, Czochralski crystal growth and many other fluid-dynamical systems and biological systems) which exhibit significant spatial variations due to presence of strong diffusive and convective terms.
One of the widely used technique for problems with nonlinear spatial differential operators or to problems defined over irregular spatial domains is a data-driven method know as the method of snapshots -also known as proper orthogonal decomposition (POD)- which is based on Karhunen-Loève expansions. This method has been extensively utilized to "empirically" compute the eigenfunctions using an ensemble of solution data obtained either through experimental observations or from detailed numerical simulations.
It has been widely used in model reduction, optimization, sensor placement and control of distributed processes. Note though that this approach however rely on the a priori availability of a large ensemble of PDE solution data (snapshots) in which all the possible spatial modes have been excited. (That is all the expected process should be known, to be assured that the process model found using these eigenfunction remains valid throughout the process operation). Unfortunately, no well defined methodology exists for generating such an ensemble.
Our work focuses on developing and applying of adaptive model reduction methodology which doesn’t need a large ensemble of PDE solution data! This adaptive model reduction methodology, coined Adaptive Proper Orthogonal Decomposition (APOD) allows us to design feedback controllers for transport reaction and fluid flow systems described by PDE systems.
The novelty of our approach lies in that we do not require the availability of spectral eigenfunctions or well constructed data ensembles as previously required in the literature. Rather we recursively update the initially computed eigenfunctions as process, under the command of the controller, moves through different regions of state space. For an introduction to the concept of APOD please refer to A. Varshney, S. Pitchaiah and A. Armaou, AIChE J., 55:906-918, 2009. Different interesting and valuable applications involving advanced process control and optimization are being pursued.
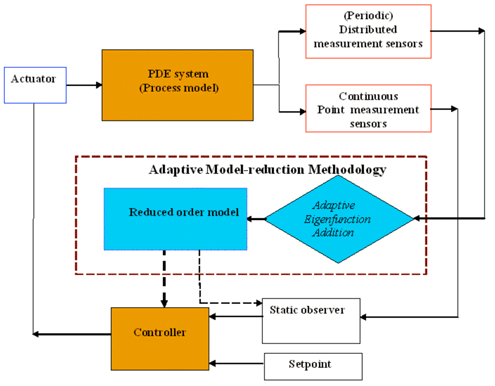
Block diagram of the Adaptive Proper Orthogonal Decomposition (APOD)
Illustrattive application to Kuramoto-Sivashinsky equation: The ability of APOD along with an output feedback controller in stabilizing processes is illustrated on the Kuramoto-Sivashinsky equation (KSE), where the control objective is to reach the steady state x(z,t)=0. KSE involves non-trivial dynamics with the existence of steady and periodic wave solutions, as well as chaotic behavior. KSE can adequately describe incipient instabilities arising in a variety of physico-chemical systems including falling liquid films, unstable flame fronts and interfacial instabilities between two viscous fluids.
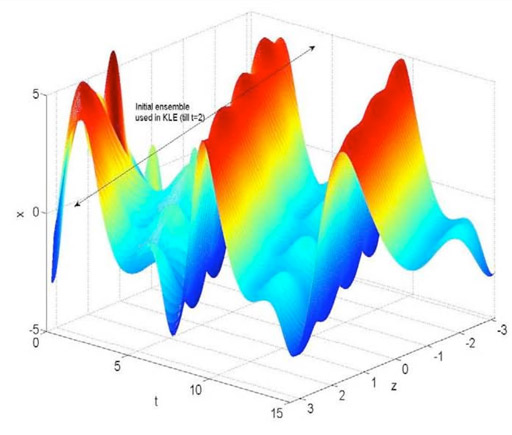
Open-loop KSE.
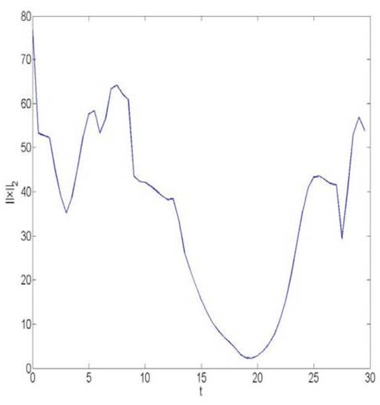
CLosed-loop 1_2 norm with out APOD & Lyapunov based nonlinear controller.
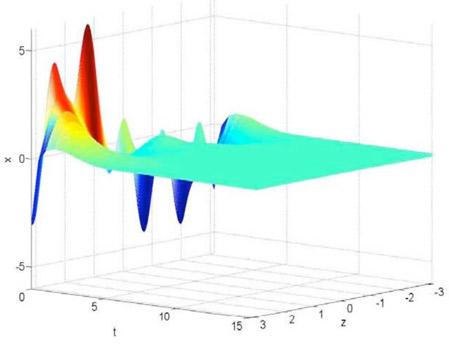
Closed-loop KSE using APOD & Lyapunov based nonlinear controller.

Closed-loop 1_2 norm with APOD & Lyapunov based nonlinear controller.
Page created on 02/24/11, Top of page


